Concurrency Control for Database Transactions
来自 DATABASE SYSTEMS: The Complete Book
Serial and Serializable Schedules⌗
Serial schedule: no mixing of actions from different transactions.
Serializable schedule: if there is a serial schedule S’ such that for every initial database state, the effects of S and S’ are the same.

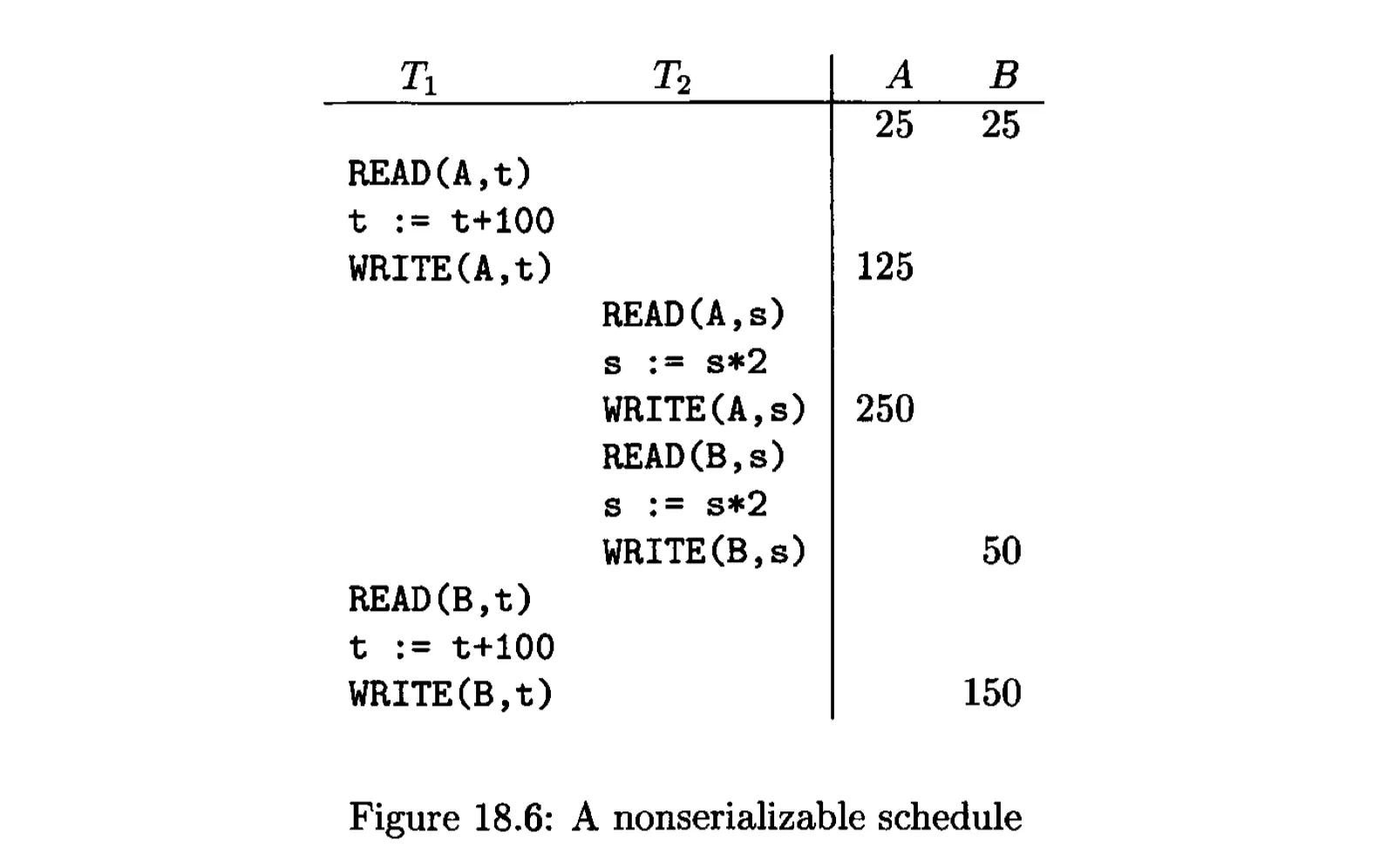
The details of the transactions do matter, but it is not realistic for the scheduler to concern itself with the details of computation undertaken by transactions.
We only care about the reads $r_T(X)$ and writes $w_T(X)$ performed by the transaction $T$.
Conflict-Serializability⌗
Actions that conflict (i.e. their order may not be swapped):
- Two actions of the same transaction.
- Two writes of the same database element by different transactions.
- A read and a write of the same database element by different transactions.
In other words, for actions from different transactions, they conflict when:
- They involve the same database element, and
- At least one is a write.
Conflict-equivalent: two schedules can be turned one into the other by a sequence of nonconflicting swaps of adjacent actions.
Conflict-serializable: the schedule is conflict-equivalent to a serial schedule
conflict-serializability $\Rightarrow$ serializability
Precedence: if there are actions $A_1$ of $T_1$ and $A_2$ of $T_2$, such that:
- $A_1$ is ahead of $A_2$ in the schedule $S$,
- Both $A_1$ and $A_2$ involve the same database element, and
- At least one of $A_1$ and $A_2$ is a write action.
then we say that $T_1$ takes precedence over $T_2$ in $S$ ($T_1<_ST_2$).
Any conflict-equivalent serial schedule must have $T_1$ before $T_2$.
If the precedence graph is acyclic, then the schedule is conflict-equivalent.
Proof: for $n$, arrange the schedule by (Actions of $T_i$)(Actions of the other $n-1$ transactions) where $T_i$ is one node without an in arc.
Enforcing Serializability by Locks⌗
The use of lock:
- Consistency of Transactions: Actions and locks must relate in the expected ways:
- A transaction can only read or write an element if it previously was granted a lock on that element and hasn’t yet released the lock.
- If a transaction locks an element, it must later unlock that element.
- Legality of Schedules: Locks must have their intended meaning: no two transactions may have locked the same element without one having first released the lock.
The two-phase locking condition than can ensure conflict-serializability:
- In every transaction, all lock actions precede all unlock actions.
A transaction that obeys the 2PL condition is said to be a two-phase-locked transaction, or 2PL transaction.
Proof: for $n$, arrange the schedule by (Actions of $T_i$)(Actions of the other $n-1$ transactions) where $T_i$ is the transaction with the first unlock action $u_iX$.
The risk of deadlock:

Locking Systems With Several Lock Modes⌗
Lock modes:
- shared
- exclusive
The compatibility matrix:
| Request S | Request X | |
|---|---|---|
| Currently S | Yes | No |
| Currently X | No | No |
The deadlock problem caused by upgrading locks:

Avoid the problem with a third lock mode: update locks.
- An update lock $ul_i(X)$ gives transaction $T_j$ only the privilege to read X, not to write X;
- Only the update lock can be upgraded to a write lock later; a read lock cannot be upgraded.
The compatibility matrix:
| Request S | Request X | Request U | |
|---|---|---|---|
| Currently S | Yes | No | Yes |
| Currently X | No | No | No |
| Currently U | No | No | No |
The columns for U and S locks are the same, and the rows for U and X locks are the same.
And now:

An Architecture for a Locking Scheduler⌗
The architecture discussed here: the scheduler insert and release locks.
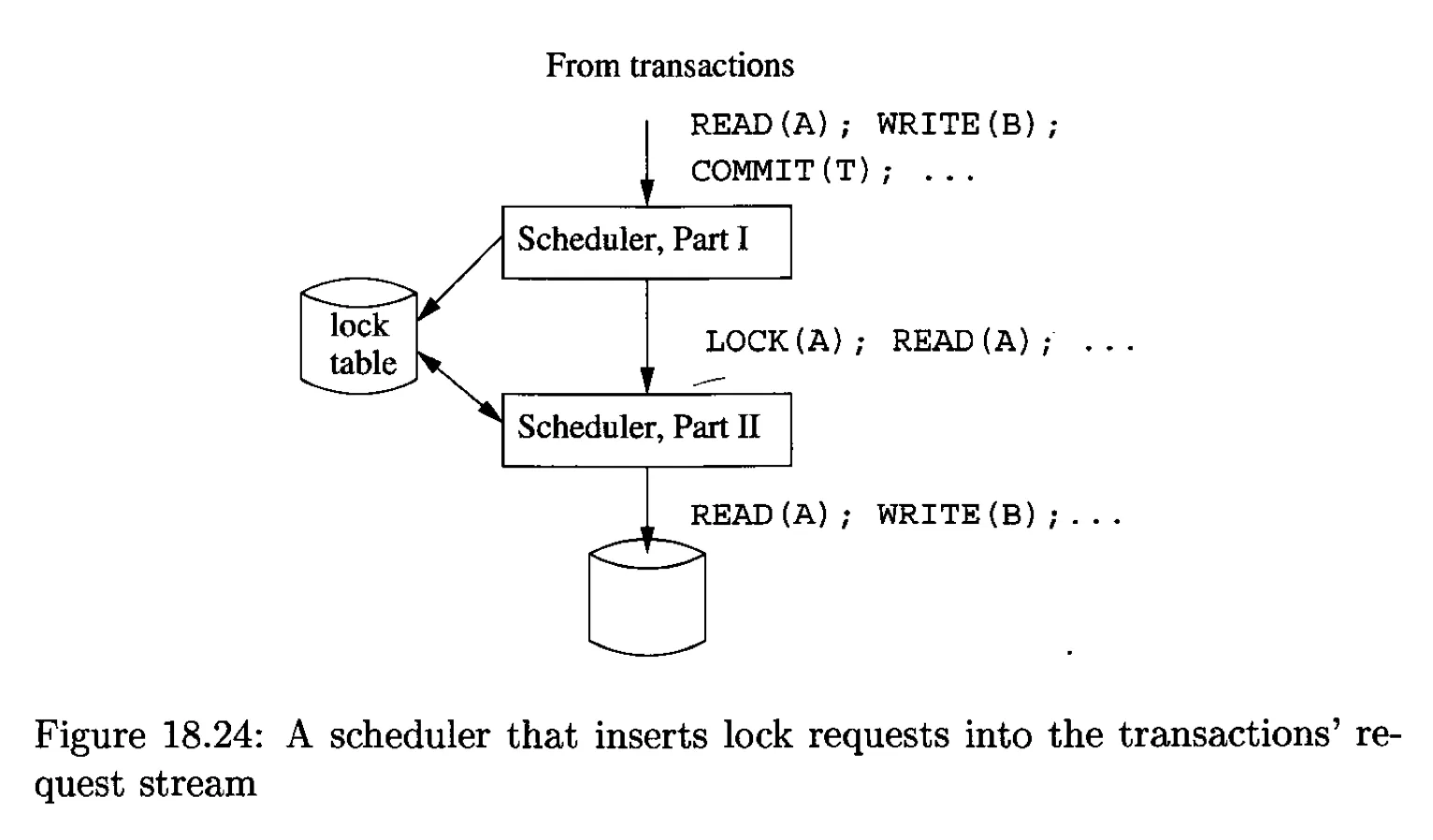
- Part 1: inserts appropriate lock actions ahead of all database-access operations
- Part 2: for received action,
- if the issuing transcation is already delayed, then delay this action
- otherwise,
- if the action is db access (the required locks are already been granted), execute it
- if is lock action
- if the lock can be granted: modify the lock table
- otherwise, request the lock and delay
- When a transcation commits or aborts, Part 1 releases all locks held by the transaction; if any transactions are waiting for any of these locks, notify Part 2
- Part 2 checks which actions can be executed now
The lock table entry:
- The group mode: the most stringent conditions
- The waiting bit: at least one transaction is waiting
- A list of transactions that hold or waiting for the lock
Hierarchies of Database Elements⌗
Warning locks: useful for hierarchical structure.
| IS | IX | S | X | |
|---|---|---|---|---|
| IS | Yes | Yes | Yes | No |
| IX | Yes | Yes | No | No |
| S | Yes | No | Yes | No |
| X | No | No | No | No |
The phantom tuple: one that should have been locked but wasn’t, because it didn’t exist at the time the locks were taken.
Solution: acquire an X lock on the entire relation.
The Tree Protocol⌗
The problem: only one transaction that is not read-only can access the B-tree at any time, because the root node must be locked (at least with an update lock).
Solution: as soon as a transaction moves to a child of the root and observes the (quite usual) situation that rules out a rewrite of the root, we would like to release the lock on the root; but it violates 2PL, so a new protocol is needed.
The tree protocol:
- The schedule is legal (i.e. does not violate lock schemes).
- A transaction’s first lock may be at any node of the tree.
- Subsequent locks may only be acquired if the transaction currently has a lock on the parent node.
- Nodes may be unlocked at any time.
- A transaction may not relock a node on which it has released a lock, even if it still holds a lock on the node’s parent.
Conclusion: the precedence graph must always be acyclic if the tree protocol is obeyed. Proof:
- If two transactions lock several elements in common, then they are all locked in the same order.
- If $T_i$ locks the root before $T_j$, then $T_i$ locks every node in common with $T_j$ before $T_j$ does.
Concurrency Control by Timestamps⌗
Two approaches to generate timestamp:
- use the system clock
- the scheduler maintaining a counter
For the database element $X$:
- $RT(X)$: the read time of $X$
- $WT(X)$: the write time of $X$
- $C(X)$: the commit bit fot $X$, true when the most recent transaction to write $X$ has already commited.
Two kinds of unrealizable behaviours:
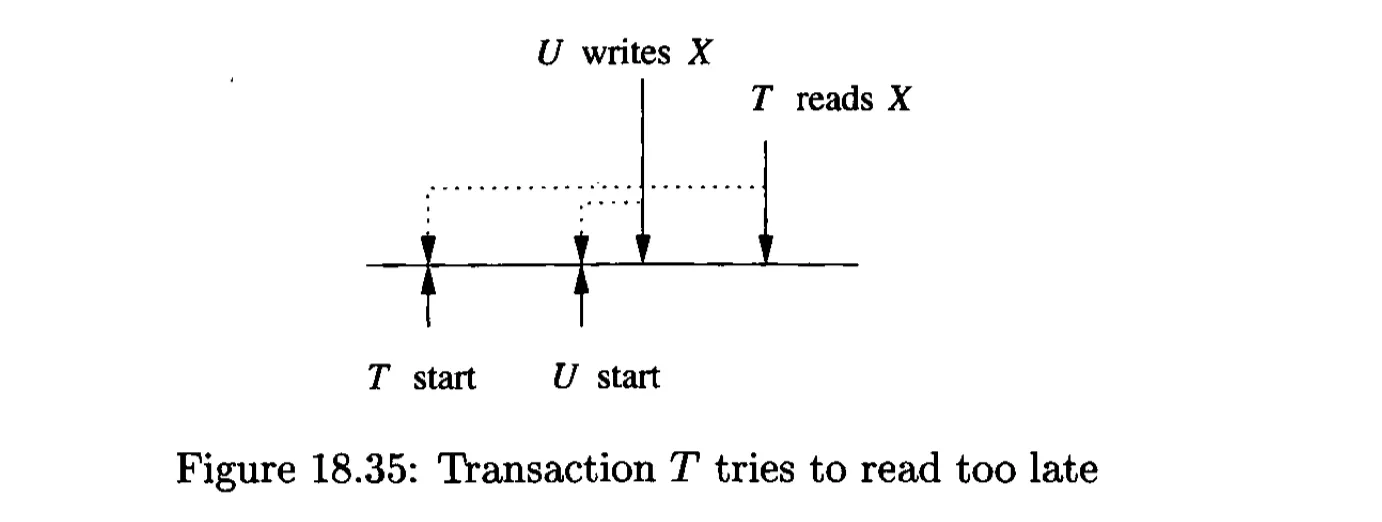
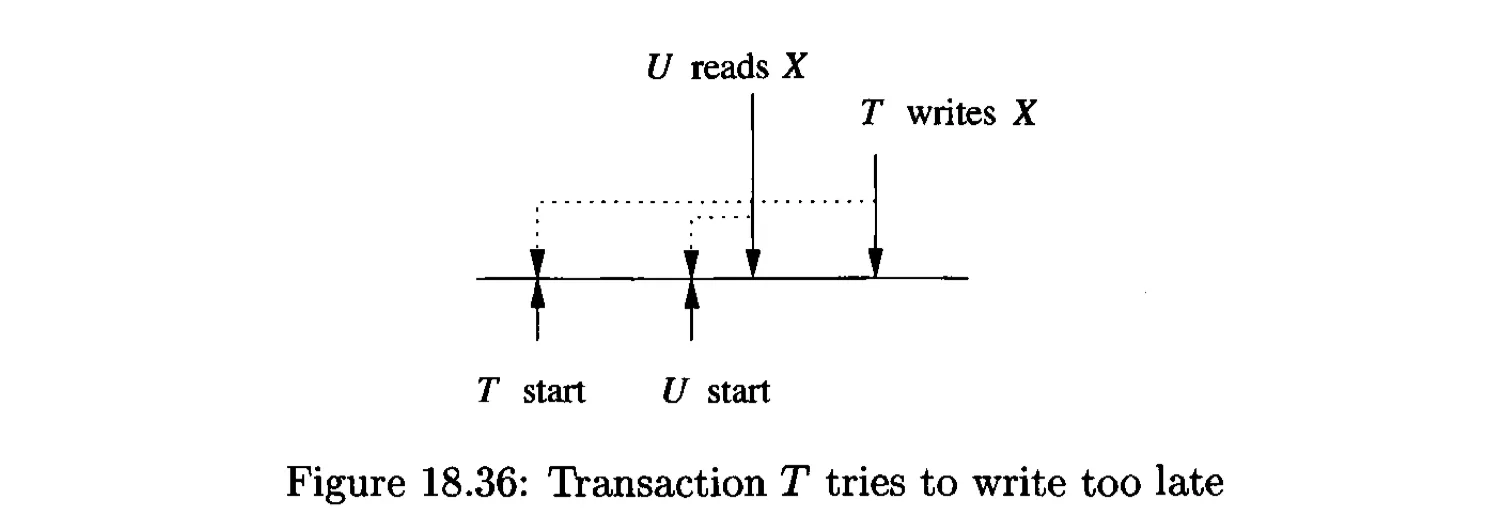
The problem with dirty data:
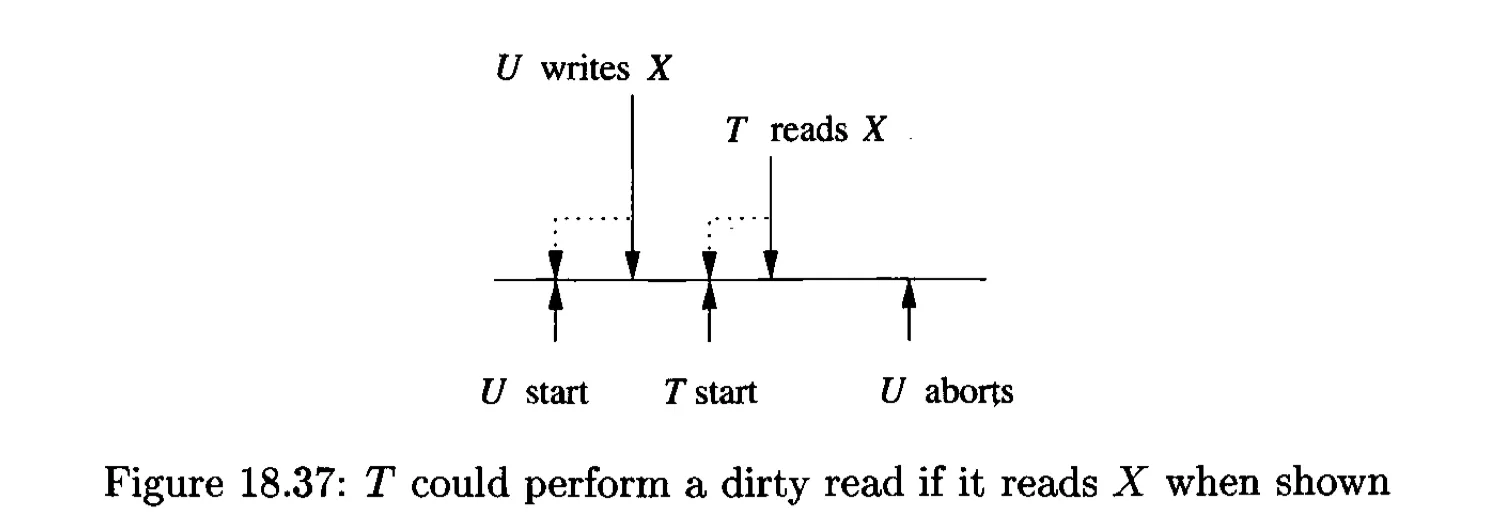
$T$ better delays until $U$ commits.
The commit bit will be false.
The Thomas write rule: the writes can be skipped when a write with a later write-time is already in place (read intention for value written by T is too-late, as the value is written by a logically latter transaction).
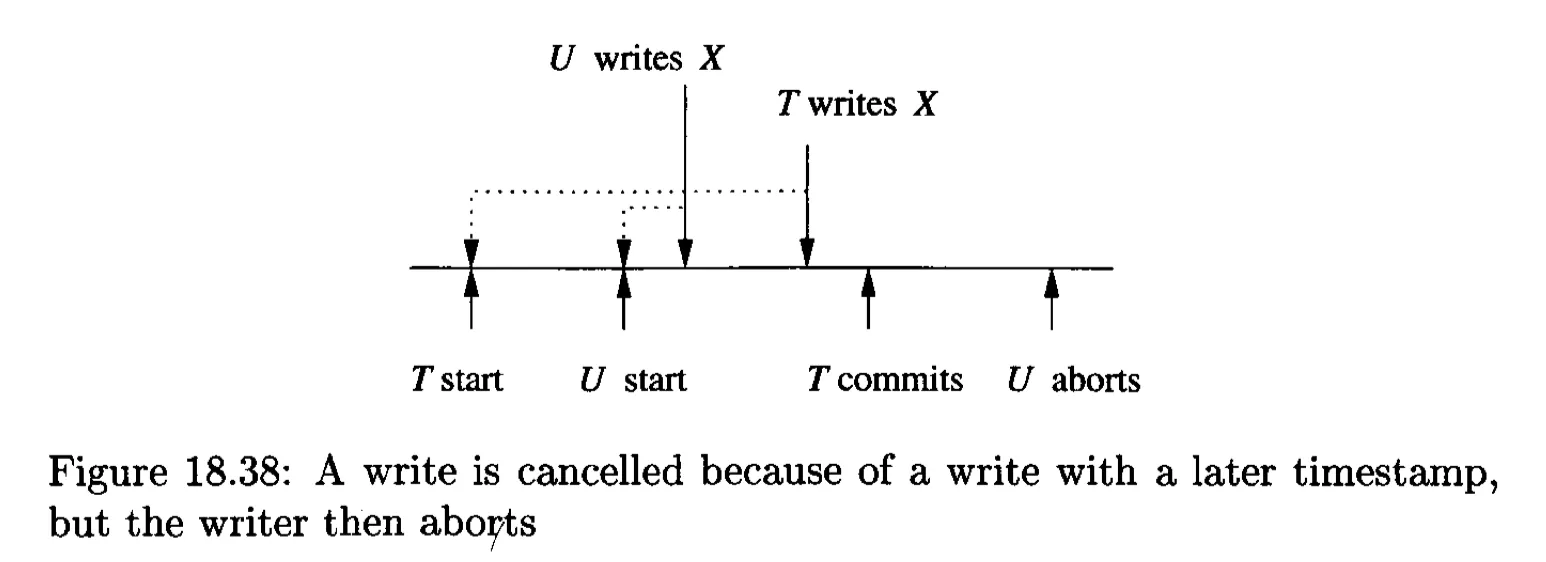
The scheduler, in response to a read or write request from a transaction T has the choice of:
- Granting the request,
- Aborting T and restarting T with a new timestamp
- Delaying T and later deciding whether to abort or grant the request.
The rules for timestamp-based scheduling:
- The scheduler receives a request $r_T(X)$.
- $TS(T)\ge WT(X)$: physically realizable.
- $C(X)$ is true: grant the request; set $RT(X)$ if $TS(T)>RT(X)$.
- $C(X)$ is false: delay until becomes true, or that transaction aborts (to avoid dirty reads).
- $TS(T)<WT(X)$: physically unrealizable, rollback $T$.
- $TS(T)\ge WT(X)$: physically realizable.
- The scheduler receives a request $w_T(X)$.
- $TS(T) \ge RT(X)$ and $TS(T) > WT(X)$: physically realizable and must be performed (?).
- Write $X$,
- Set $WT(X) := TS(T)$, and
- Set $C(X) := \texttt{false}$.
- $TS(T) \ge RT(X)$ but $TS(T) < WT(X)$: physically realizable, and
- If $C(X)$ is true, ignore the write by T (the thomas write rule);
- otherwise, delay T until the previous write operation commits or aborts.
- $TS(T) < RT(X)$: physically unrealizable, roll back T.
- $TS(T) \ge RT(X)$ and $TS(T) > WT(X)$: physically realizable and must be performed (?).
- The scheduler receives a request to commit T: find all elements written by T, and set $C(X) := \texttt{true}$; the delayed transactions are allowed to proceed.
- The scheduler receives a request to abort T, or to rollback: check all delaying transcation waiting for any element that T wrote to see if they can proceed.
The use of multiversion timestamps: to provide an appropriate version for a read action (the version of X written immediately before T theoretically executed), even if the latest version is written after the transcation.
Comparision of locking and timestamp schemes:
Generally, timestamping is superior in situations where either most transactions are read-only, or it is rare that concurrent transactions will try to read and write the same element. In high-conflict situations, locking performs better.
- Locking will frequently delay transactions as they wait for locks.
- If concurrent transactions frequently read and write elements in common, then rollbacks will be frequent in a timestamp scheduler.
Concurrency Control by Validation⌗
Validation differs from timestamping principally in that the scheduler maintains a record of what active transactions are doing, rather than keeping read and write times for all database elements.
Denote the write set and read set as $WS(T)$ and $RS(T)$. Transactions are executed in three phases:
- Read. The transaction reads from the database all the elements in its read set, and also computes (locally) the results it is going to write.
- Validate. The transaction compares its read and write sets with those of other transactions; rollback if fails.
- Write. The transaction writes to the database the values for the elements in its write set.
Thus, the validation-based scheduler has an assumed serial order of the transactions to work with, and it bases its decision to validate or not on whether the transactions’ behaviors are consistent with this serial order.
The scheduler maintains three sets:
- START: the set of transactions that have started, but not yet completed validation.
- VAL: the set of transactions that have been validated but not yet finished the writing in phase 3.
- FIN: the set of transactions that have completed phase 3.
Some examples:
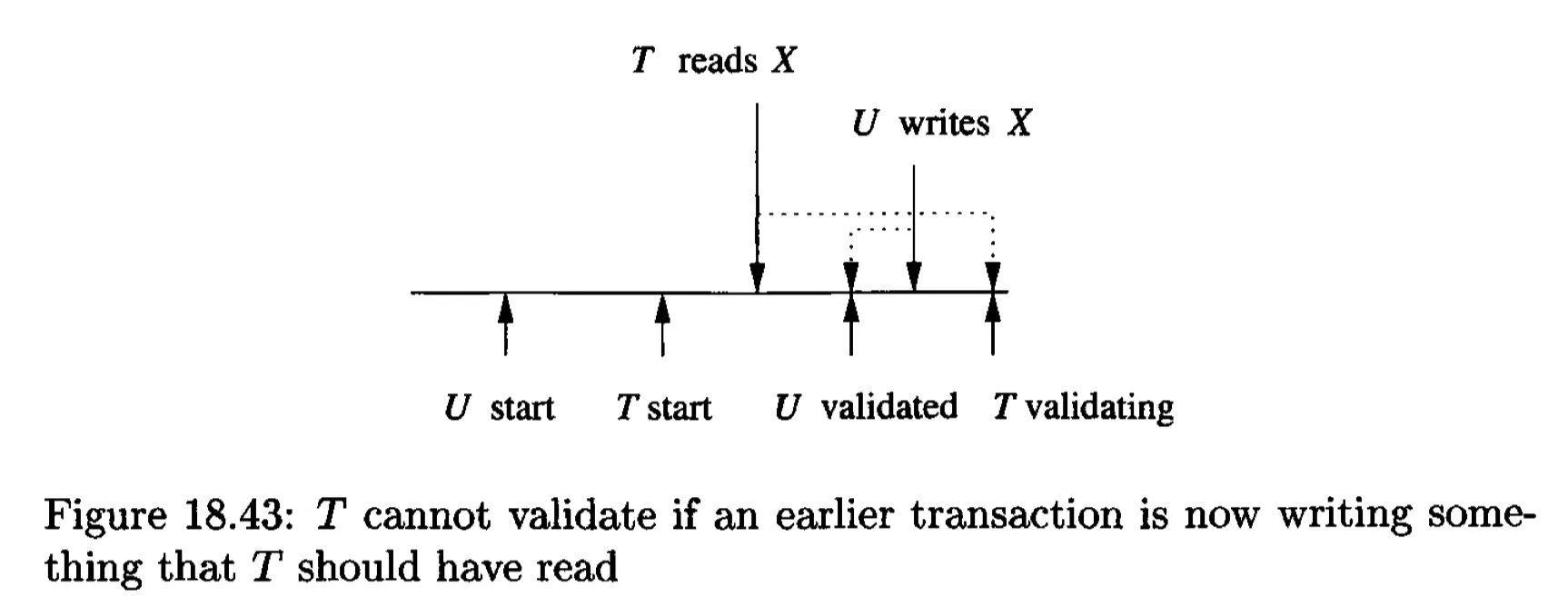
A later transaction might read a value before an earlier transaction writes the value.
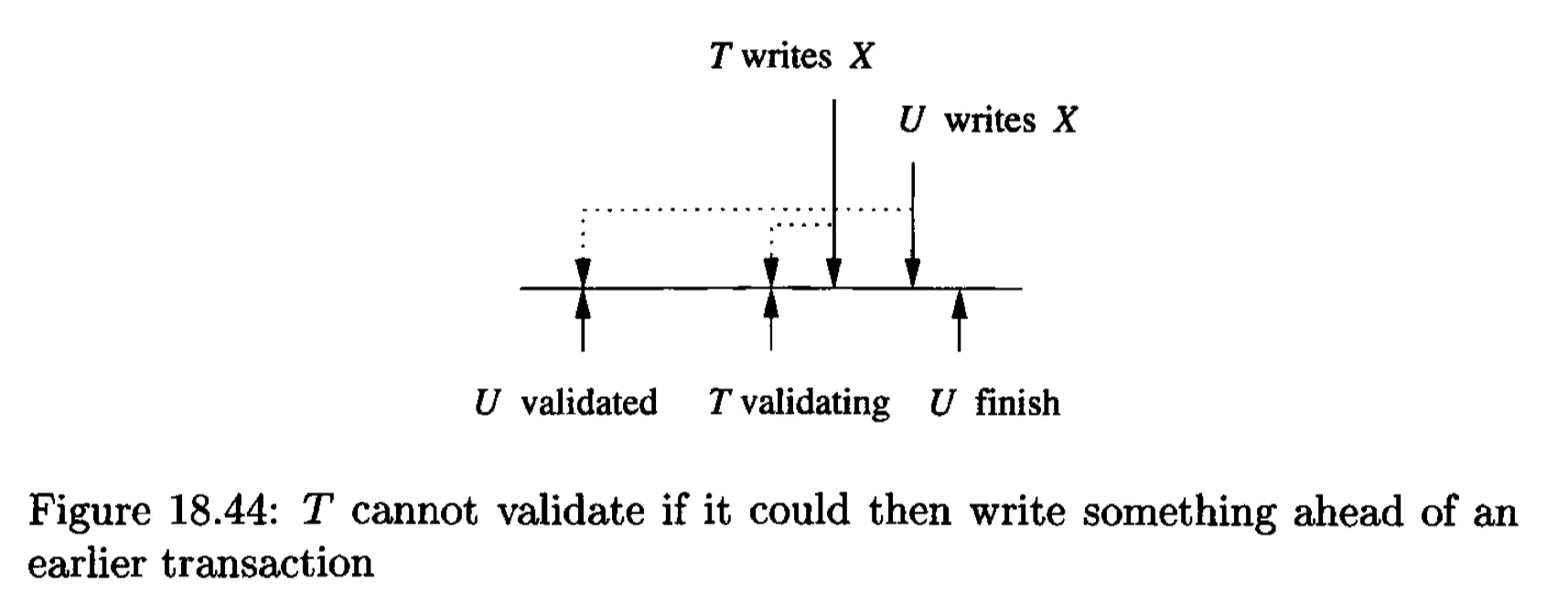
A later transaction might write before a validated, earlier transaction, as the write of the later one might occur earlier.
Summarization: to validate a transaction T:
- Check that $RS(T) \cap WS(U) = \emptyset$ for any previously validated U that did not finish before T started, i.e., if $FIN(U) > START(T)$.
- Check that $WS(T) \cap WS(U) = \emptyset$ for any previously validated U that did not finish before T validated, i.e., if $FIN(U) > VAL(T)$.
Comparison of Three Concurrency-Control Mechanisms⌗
Storage: all schemes (can be optimized to) use storage space proportional to the sum over all active transactions of the number of database elements the transaction accesses.
Performace:
- Locking delays transactions but avoids rollbacks, even when interaction is high.
- Timestamps and validation do not delay transactions, but can cause them to rollback.
- If interference is low, then neither timestamps nor validation will cause many rollbacks, and may be preferable to locking because they generally have lower overhead than a locking scheduler.
- When a rollback is necessary, timestamps catch some problems earlier than validation, which always lets a transaction do all its internal work before considering whether the transaction must rollback.
总结⌗
同时执行多个事务时,需要保证每个事务的原子性,同时还必须保持一定的先后次序。
对 schedule 最严格的要求是串行性(serial),当然这并不能做到并发。退一步,我们不需要严格保证不同事务处理的时间不互相重叠,但需要保证最终的效果和串行执行一致,即“可串行化”(serializable schedule)。当然,这个条件覆盖的范围太大,很难判断 schedule 是否满足可串行化条件。因此,我们需要增加更严格的条件,使得我们可以有简单的方法判断。当然,这样一来,满足条件的 schedule 只是可串行化 schedule 的一个真子集。
第一大类办法是使用锁,并加上 2PL 条件,使得 schedule 满足“冲突可串行化”(confilict-serializable)。上锁有两个需要解决的问题:锁的类型及其兼容性,以及锁的粒度。
第二大类办法是“乐观的”(optimistic),即假设不会发生不可串行化的事件,仅当的确出现违反可串行化条件时采取措施。Optimistic 方法包括两种:by timestamp,即通过比较事务开始的时间与元素被读或写的时间,判断某个操作是否可以进行;by validation,即在验证阶段比较与之前事务的读写集合判断是否可以提交,验证成功后再写入数据库。
上锁的方法避免了重新执行,但事务会受到延迟,在冲突严重时较优;乐观方法由于可以进行一定操作,只在出现问题时取消或重新执行,因此延迟较低,但在冲突严重时会造成大量的重新执行而影响性能。